3D Reconstruction: Triangulate points. The End
¿Where do we stay on our way to 3D reconstruction?
After computing the epipolar fringe, we find in it the homologous of our characteristic point obtained in the first post.
And now what?
We are now reaching the last bend in our path to the 3D reconstruction.
The next and last step is triangulation, which consists of computing the 3D point that corresponds to the paired homologous points. For this, the projection matrices of both cameras are used which are available because the scene has been previously calibrated.
Using the theory of epipolar geometry, we can affirm that the projection matrix complies with the following formula:
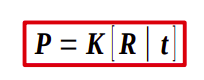
With the previous equation and the definition of the homologous points through their visuals, the following system of equation is obtained, that will be solved through algebraic minimization.
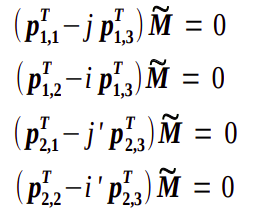
Taking into account the above theory, we performed the reconstruction of the scene in 3D. The final result is shown in the following image:
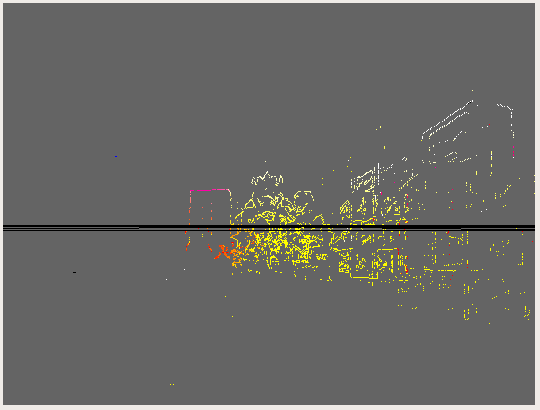
Inference:
After carrying out the development of this project and submitting it to evaluation, it has been possible to verify several questions that, due to their importance in this type of 3D reconstruction systems, are worth highlighting.
- The 3D reconstruction process using stereo vision cameras is computationally quite expensive. 30 min in this case.
- Having two 2D images and the calibration of the cameras you can extract information from the reality presented in 3D, such as depth.
- The selection of good characteristic points is crucial so that the reconstructed image remains consistent.
- Epipolar geometry is the main baseline of any 3D reconstruction through a stereo vision system
Improvements to consider in the future:
If you have time to work development more deeply, it may be interesting to take the following steps:
- To improve computational cost: The time it takes to reconstruct the scene is very high mainly due to the computational cost used in presenting the points obtained as a result. Therefore, it is proposed to save the points in a numpy array, and present them all at once in the last run.
- The simulation system suffers from constant movement that slowly rotates the camera. This causes distortion in the calculated points, although an attempt has been made to reset the position of the cameras from time to time. A simulator that does not perform this movement will present a more realistic 3D reconstruction.
- The result obtained by the OpenCv function cv2.matcheTemplate is not the best. An alternative development can be considered to carry out this step.
This project has come to an end and with it the course. It has been a pleasure to share these developments with you and we hope that they have been useful for your projects.
